機械学習を利用して、バタイユゲームのデータから史実の勝敗を予想してみる。
もちろん、ゲームの勝敗は無理である。しかし、ゲームが再現しようとしている環境
から史実の勝敗が予想できるのか興味があった。そこで、試してみた。
1.基本データ
バタイユゲーム情報班のホームページで紹介してきたゲーム概要に
次の情報が入っている。
・ゲームマップ :縦横のHEX数
・ゲームユニット:両軍の歩兵大隊、騎兵連隊、砲兵中隊の数
・ゲームターン:メインシナリオのターン数(時間に相当)
・史実データ:勝利者、フランス軍と連合軍の司令官
2.参考にした機械学習
実践 ロジスティック回帰である。ここでは、キノコのデータから毒キノコか
食用キノコかの分類問題が説明されている。
同様に上記1の基本データを基に、未知のゲームの史実勝敗を予測する。
なお、ロジスティク回帰は2択の分類である。そこで、今回は、次の2段階で
勝敗を予想する。
・勝つかどうかの2択で分類(”勝ち” と ”引き分けか負け”)
・負けるかどうかの2択で分類(”負け” と ”引き分けか勝ち”)
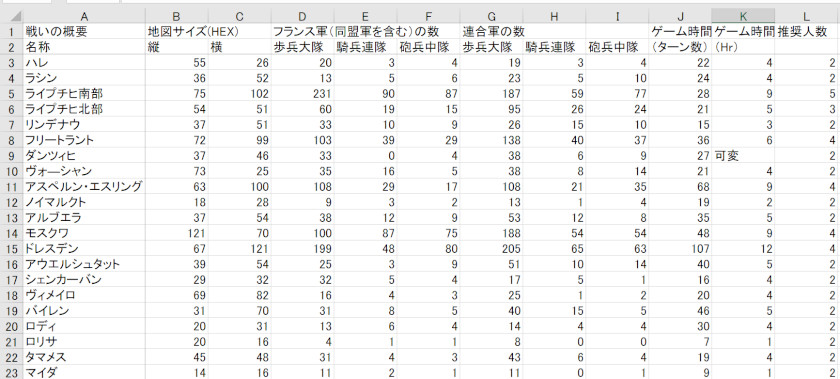
3.入力データ
下図のファイルをcsvファイルで保存したもの。(コードをUTF-8に変更)
なお、不要な標題や不備のデータは、pythonのプログラムで削除する事にした。
前回のバタイユゲームのプレイ時間予想で使った下記(A)のデータの他に(B)を追加している。
(A)戦場の大きさ、両軍の規模、戦いの時間
(B)両軍の司令官・国、と勝利者
データが不足して除外するアブキールを除くと、フランス軍の勝ち、負け、引き分けの数は、
28勝14敗6引き分けである。
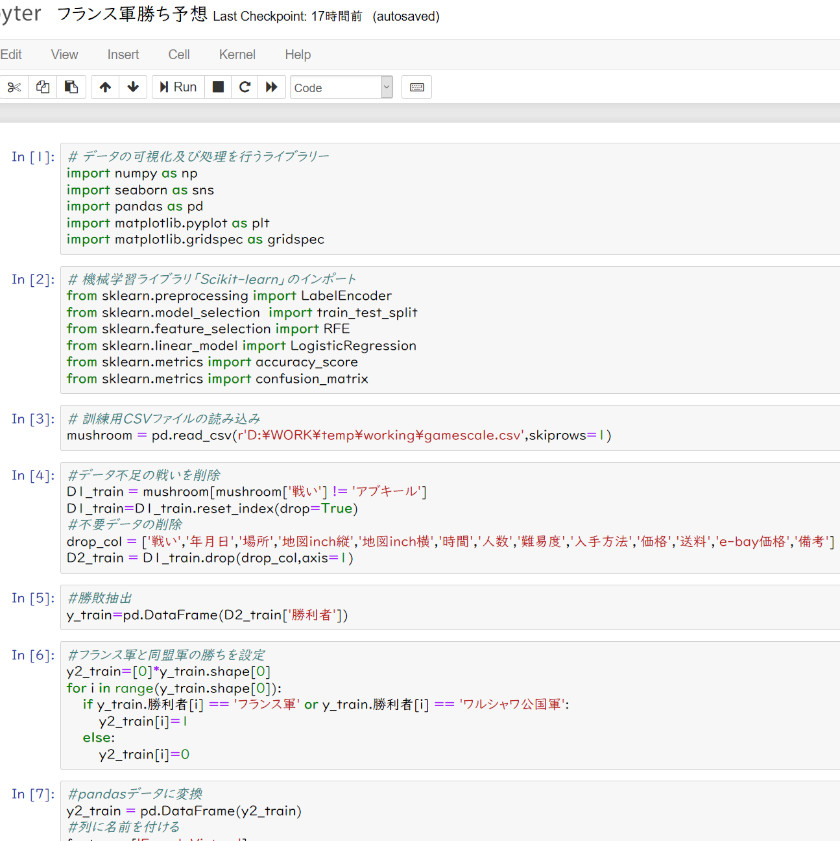
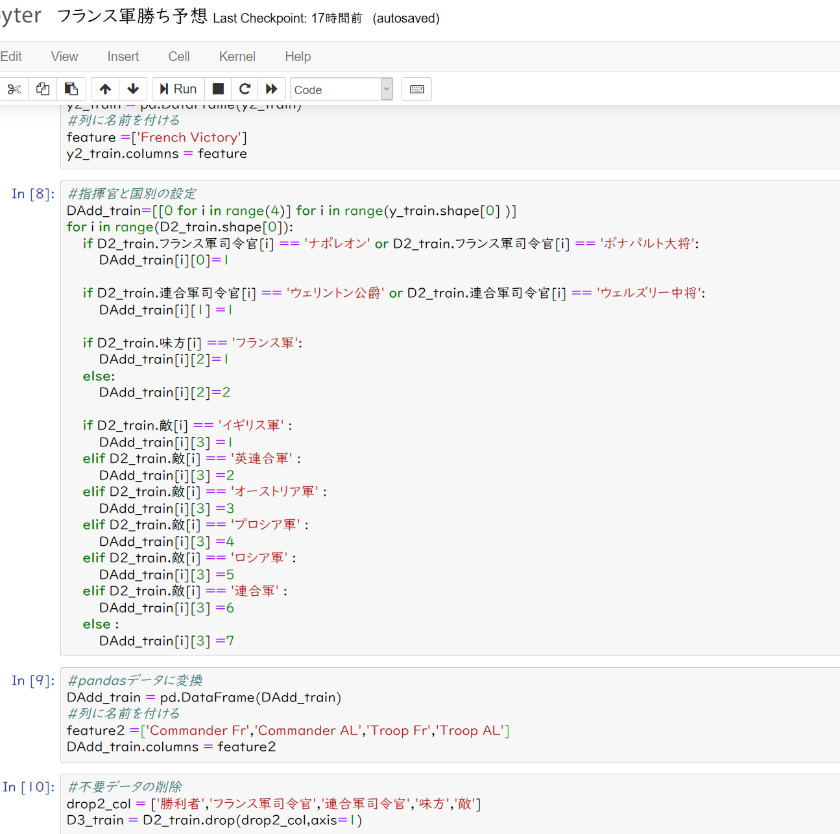
4.JupyterNotebookでコーディングした例
(1)フランス軍の勝ち予想
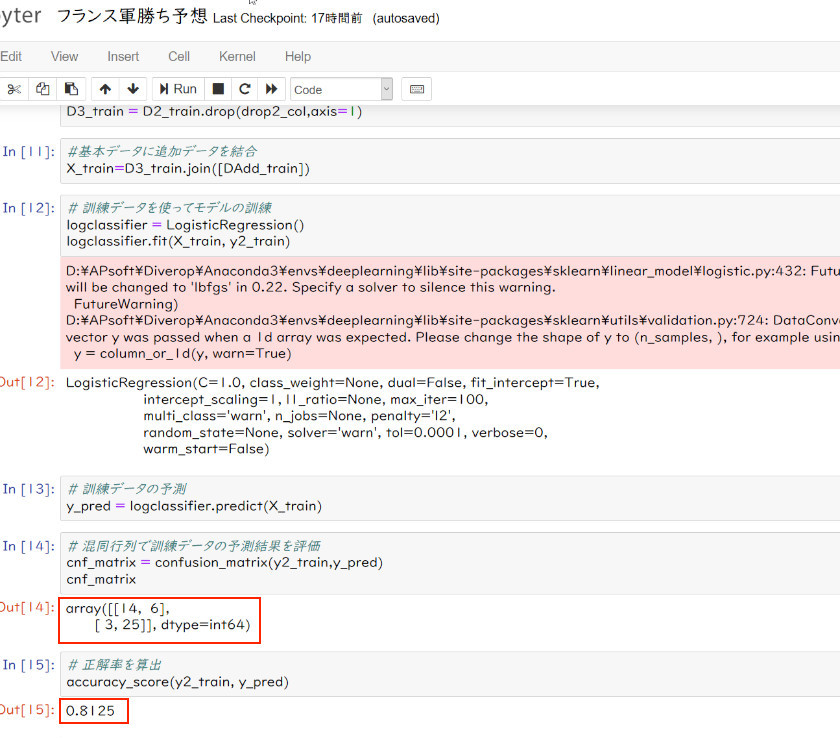
上図赤枠の混同行列array([[14,6],[3,25])とあるが、この数字の意味は次の通りである。
史実が勝ち以外の場合(20)> 予想が勝ち以外となったが14、 予想が勝ちとなったのが6
史実が勝ちの場合(28)> 予想が勝ち以外となったのが3、 予想が勝ちとなったのが25
このモデルの性能評価は、以下の通り。いずれも80%を超えており、悪くない。
正解率=(勝ち以外と勝ちの正しい予想数)÷(全体の予想数)
=(14+25)÷(14+6+3+25)=0.8125
勝ちの適合率=(勝ちの正しい予想数)÷(勝ちの予想数)
=25÷(6+25)=0.8085
勝ちの再現率=(勝ちの正しい予想数)÷(史実の勝ち数)
=25÷(3+25)=0.8929
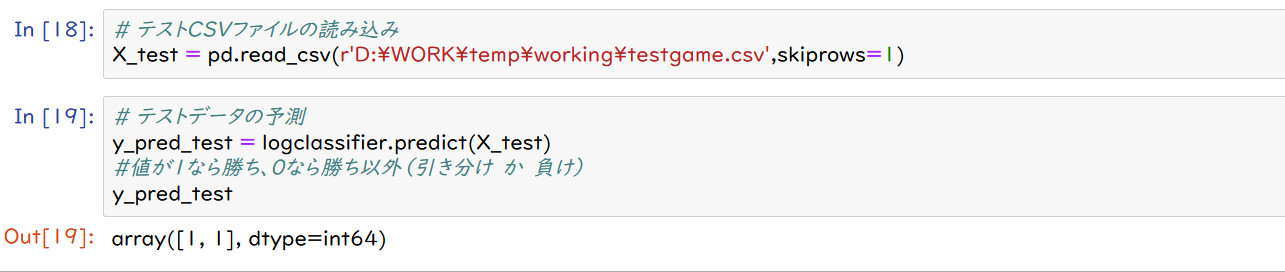
下図は、2つのゲームについて予想したものである。1番目は未知の(訓練データに含めていない)ノーヴィ、
2番目は訓練データに含めたシェンカーバンである。
予想はどちらも勝利(array[1,1]で1番目が1(勝ち)、2番めも1(勝ち))である。
史実は、2つとも勝ち以外なので、的中率は0%である。
次回へつづく
<個人的な感想>
思った以上に、訓練データの正解率が81.25%と高い。しかし、ノーヴィとシェンカーバンで予想が
外れたのは残念である(勝ちの適合率が80.85%なのに・・・)。