各種ゲームの支援ツールで使ってきた乱数はメルセンヌ・ツィスタである。
しかし、特定のゲームについては他の方法も試してみる事にした。
1.背景
今までは何の不都合も感じなかったが、Intercepter Ace支援ツールで
同じデータが4連続して表示された事に違和感を感じた。
Intercepter Aceのような1つのユニットについて物語のような流れの
ゲームについては、同じ賽の目の連続は影響が大きい。
バタイユゲームのような多数のユニットが色々なタイミングで賽の目を
参照する場合は、同じ賽の目の連続は影響が小さい。
(他のユニットへの適用や、決めるべきデータが違うので)
そこで、現時点の疑似乱数生成法を眺めて良さそうなものを比較してみた。
2.代替候補となる疑似乱数
疑似乱数wikiなどを見て、PCG(Permuted congruential generator)と
Xorshiftの後継であるXoshiro/XoroshiroからXoshiro128+にした。
PCGはpythonの新乱数としてメルセンヌ・ツィスタに代わるものであり、
Xoshiroは最も新しいものである。
3.見直しの考え方
(1)擬似乱数の生成方法そのものを比較検討するのは難しいので、
連続する賽の目の回数に絞って比較・検討する。
→今回見直しのきっかけになったもの。
(2)使用する乱数の数は1000程度を想定する。
→違和感を感じたIntercepter Ace支援ツールでは750回の乱数を使っていた。
数値計算で使うような10万回などは想定しない。
4.結論
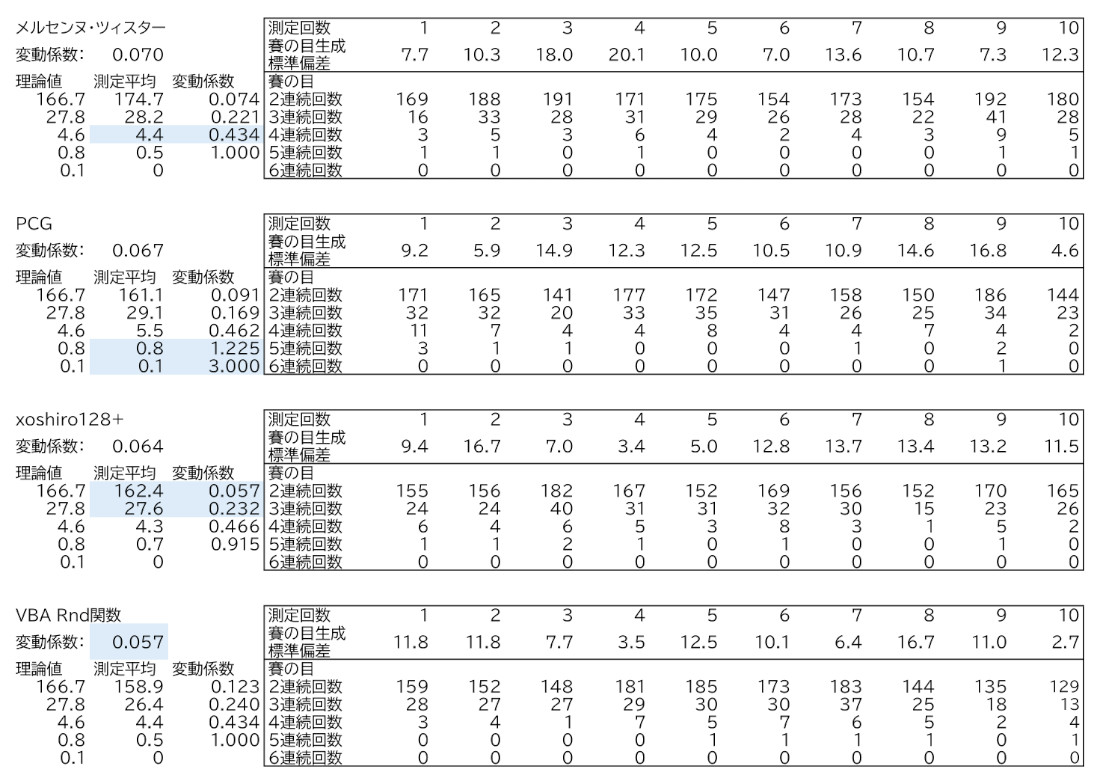
(1)下図の測定結果からXoshiro128+を代替候補とする。
測定は各候補の乱数を1000回発生させ、それを10回繰り返して平均と
標準偏差、変動係数を求めた。
(2)連続回数の測定平均が理論値に近く変動係数(ばらつき)が小さいものは薄い青を背景とした。
生成方法の下の変動係数は(例:メルセンヌ・ツィスタ0.070)”1から6の賽の目のばらつき”を示し、
測定平均の右隣は(例:メルセンヌ・ツィスタ0.434)”各連続回数のばらつき”を示している。
Xoshiro128+が一番良さそうに思う。理由は測定平均が理論値に近く、4連続以上の回数が
理論値よりも小さい(発生する確率が低い=違和感が少なく、賽の目のバラツキも小さい)。
次回へつづく
<個人的な感想>
違和感を感じた4連続同じ賽の目は、メルセンヌ・ツィスタとVBAの乱数が一番理論値に近いのが意外である。
大事な時に”たまたま出会った”事で強く印象に残ったのかもしれない。
Xoshiro128+を使ってIntercepter Aceをプレイしてみないと何ともいえない。