つづき
2.2ユニットが混乱する確率の比較
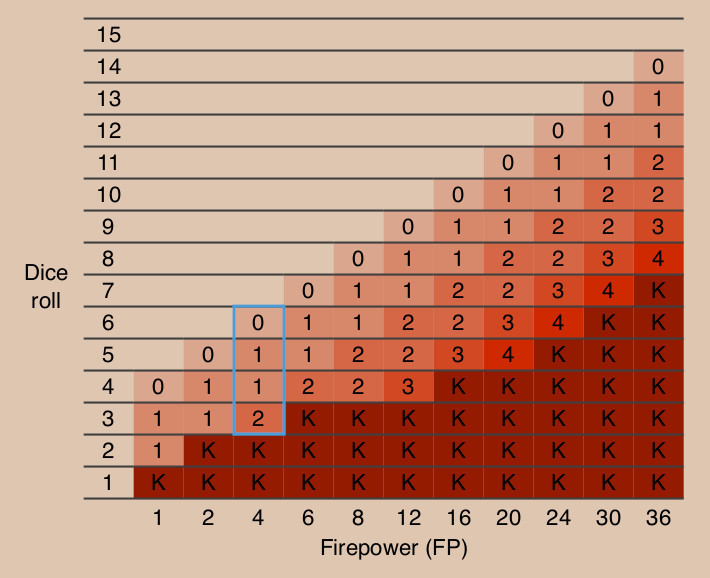
(1)Squad Leaderは、下図の枠内の場合にユニットが混乱する。
(A)平地の場合(最も損失が大きい地形)
2つの賽の目合計に-2の補正が入るので、上記の枠内に入る賽の目合計は5から8である。
賽の目合計、確率、士気補正値、士気判定失敗確率、混乱確率を計算すると以下となる。
士気補正値は賽の目(上記表では5なら-2されて3)に対する士気補正値で上記表から+2となる。
士気判定失敗確率は士気値7のユニットが士気判定に失敗する確率で、1-(士気成功確率)で計算する。
賽の目5の場合、士気成功確率は新しく振った賽の目合計+士気補正値(+2)が7以下の確率である。
賽の目合計が2から5までの確率は0.278になるので、士気判定失敗確率は1-0.278=0.722となる。
混乱確率は左記確率✕士気判定失敗確率で、賽の目5の場合は0.111×0.722=0.0802
| 賽の目合計 | 左記確率 | 士気補正値 | 士気判定失敗確率 | 混乱確率 |
| 5 | 0.111 | +2 | 0.722 | 0.0802 |
| 6 | 0.139 | +1 | 0.583 | 0.0810 |
| 7 | 0.167 | +1 | 0.583 | 0.0972 |
| 8 | 0.139 | 0 | 0.417 | 0.0579 |
| 上記全てを合計 | 0.316 |
隣接した場合は射撃力を2倍して8とするので、同様に混乱確率を計算すると0.401となる。
隣接しない場合と隣接した場合の比率を論理的に計算できないので、ここは平均して0.359とする。
(B)石の建物内の場合(最も損失が小さい地形)
上記と同様に混乱確率の平均を計算すると0.093となる。
(C)他にも色々な地形があるが、上記2つの範囲内である。そこで、平均して0.226とする。
(D)混乱は回復する可能性があるので、指揮官(士気補正値は平均値の-1を使用)の元で成功する確率である
賽の目2から8(士気補正反映)までの確率0.722を反映する。
0.226 × (1-0.722) = 0.063を試算値とする。
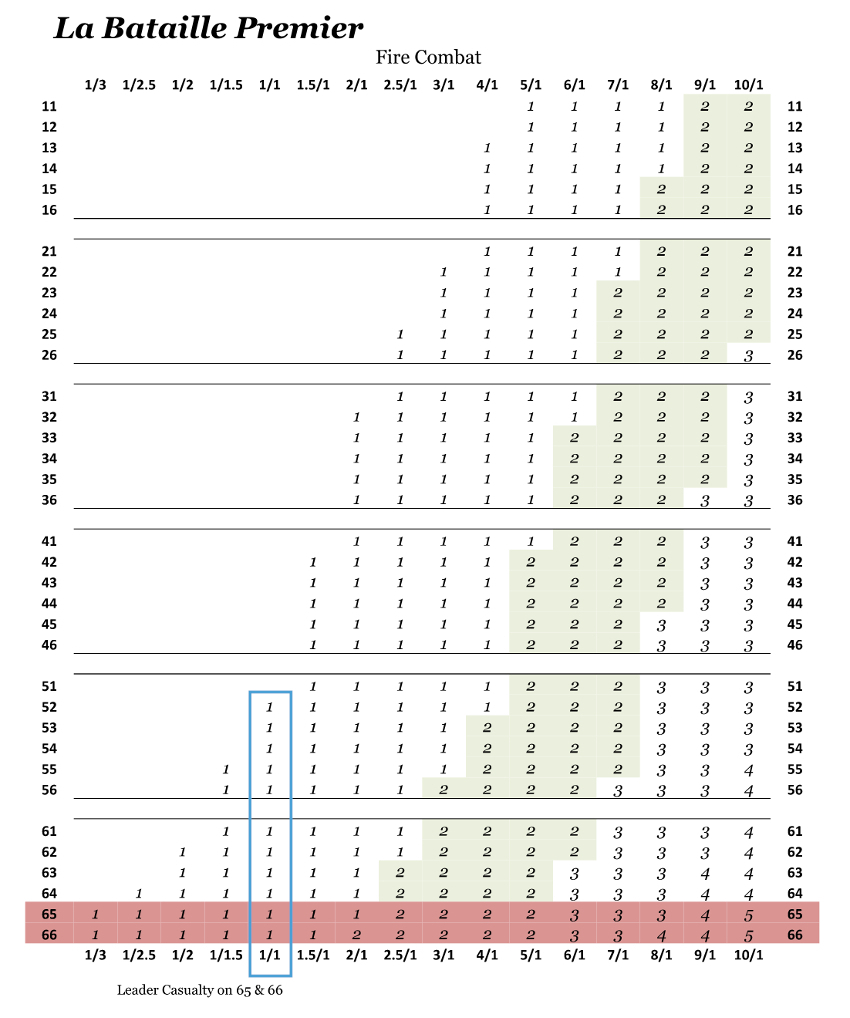
(2)バタイユゲームは、下図の枠内の場合に混乱する。(射撃で損害を受けた時に士気チェックする)
(A)平地の場合
射撃防御力が4なので、上記の枠内になる。確率は11/36=0.306となる。
士気値7のユニットが士気判定に成功する確率は、賽の目合計が2から7までの確率で0.583である。
混乱確率は0.306×(1-0.583)=0.127となる。
(B)石の建物内の場合
射撃防御力が9なので、上記表の1/2.5の欄を参照する。確率は3/36=0.083となる。
混乱確率は0.083×(1-0.583)=0.035となる。
(C)上記2つの平均値は0.081となる。
(D)混乱回復を反映した0.081 × (1-0.722) = 0.023を試算値とする。
2.3射撃戦での戦力損失確率
損失と混乱の合計を戦力損失確率とすると、
Squad Leaderは0.111 + 0.063 = 0.174
バタイユゲーム ベースは0.097 + 0.023 = 0.120
となる。
次回へつづく
<個人的な感想>
Squad Leaderはバタイユゲームに比べて混乱しやすい。
混乱を回復するキーが分隊長(Squad Leader)なので、
そのようなデザインなのだろうと思う。