下記の本を読んでいたら、p106にある”水を注ぐ関係”の問題の解決に
三角座標を使っている事に感心した。
(1)水を注ぐ関係
3つの器があり、3ℓ、5ℓ、8ℓの容量がある。8ℓの容器は満杯で、他の2つは空である。
下記の制約のもとに、4ℓづつに分けるのが問題である。
「制約」
(A)3ℓと5ℓ容器に注ぐ場合は、必ず満杯にする。
(B)但し、注ぐ元が空になれば上記を無視して良い。
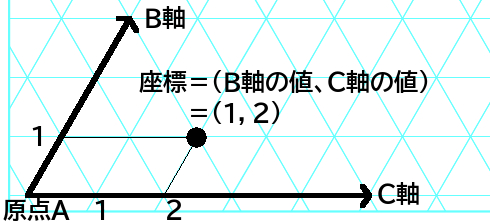
(2)三角座標
2次元で使う普通のXY座標はX軸とY軸は直角である。それに対して、三角座標は、
下記のように2つの軸が60度になっている。余り使われることがないようで、自分も知らなかった。
なお、三角方眼紙は下記のWEBページからダウンロードさせて貰いました、ありがとうございます。
(3)三角座標を使った解答
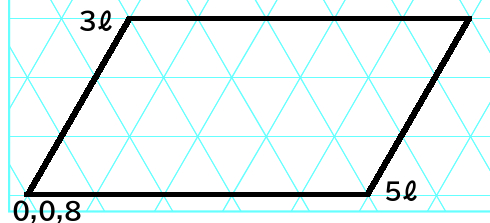
(A)準備
(a)B軸に3ℓの容器、C軸に5ℓの容器を割り当てる。
(b)すると下図のように四辺形の枠内で水の注ぎを行う事になる。
(c)8ℓの容器の水の量も気になるので、座標値の3番目に追加する。
出発点は原点(0,0,8)である。これは、8ℓの容器が満杯で、他が空である事に一致している。
(B)三角座標と水の注ぎ方の対応
(a)目標点は、上記の四辺形の枠上である。
これは、水を注ぐ場合に相手を必ず満杯にするか自分が空になる制約を反映している。
(b)各容器から水を注ぐ場合の操作と上記の座標での表し方は、以下の通り。
・3ℓの容器から5ℓの容器に注ぐ : 出発点から右下に移動し、3ℓ=0か5ℓ=5の位置で止まる。
・5ℓの容器から3ℓの容器に注ぐ : 出発点から左上に移動し、3ℓ=3か5ℓ=0の位置で止まる。
・3ℓの容器から8ℓの容器に注ぐ : 出発点から左下に移動し、3ℓ=0の位置で止まる。
・8ℓの容器から3ℓの容器に注ぐ : 出発点から右上に移動し、3ℓ=3の位置で止まる。
・5ℓの容器から8ℓの容器に注ぐ : 出発点から左に移動し、5ℓ=0の位置で止まる。
・8ℓの容器から5ℓの容器に注ぐ : 出発点から右に移動し、5ℓ=5の位置で止まる。
長くなるので、次回につづく
<個人的な感想>
上記の”水を注ぐ関係”の問題は、どのように考えて解けばよいのか、全く分からない。
試行錯誤して解答を見つけるのは気が進まないが、上記の三角座標を使った解答は
分かり易くて感心した。その方法で何故解答が見つかるのかは理解できていないが・・・。